Quantitative Genetik in der Hundezucht
Dieser Artikel führt Hundezüchter in die Grundlagen der quantitativen Genetik ein. Anhand praktischer Beispiele werden wichtige Konzepte wie Zuchtwert, Erblichkeit und genetische Korrelationen erläutert. Besonderes Augenmerk liegt dabei auf der gleichzeitigen Verbesserung mehrerer Merkmale, einer häufigen Herausforderung in der Zuchtpraxis.
0. Einleitung
„Wie die Eltern, so die Kinder“ – diese alte Züchterweisheit enthält viel Wahres, aber es gibt immer wieder Überraschungen. Jeder erfahrene Hundezüchter kennt die Situation: Ein schöner Rüde bringt keine schönen Nachkommen hervor, oder eine Hündin mit ausgezeichnetem Wesen hat Welpen mit schwierigem Charakter. Auch den umgekehrten Fall gibt es: Eine weniger vielversprechende Verpaarung bringt hervorragende Nachkommen hervor. Wie lassen sich solche Erscheinungen erklären? Und wichtiger noch: Wie können wir dieses Wissen nutzen, um gezielt auf erwünschte Eigenschaften zu züchten?
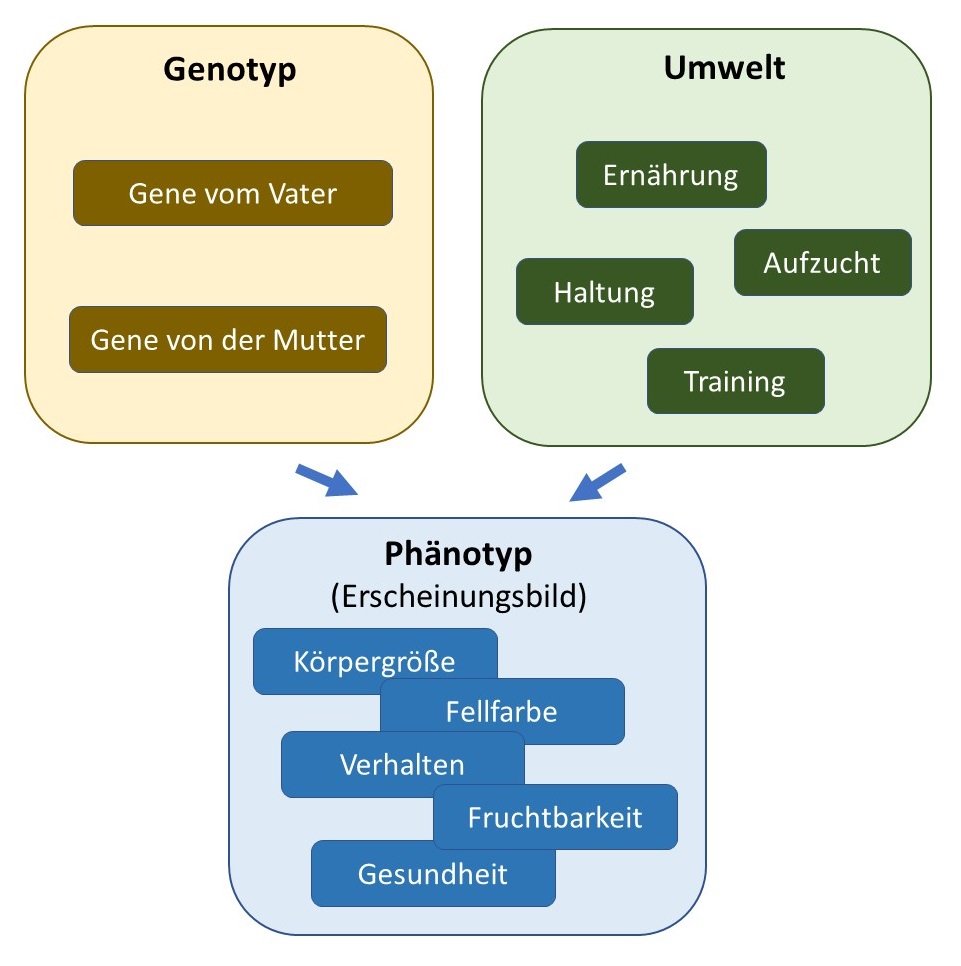
Das Erscheinungsbild wird von den Genen und von der Umwelt beeinflusst.
Die meisten für die Hundezucht wichtigen Merkmale – ob Körperformen, Gesundheitsaspekte oder Verhaltenseigenschaften – werden nicht von einem einzelnen Gen bestimmt, sondern entstehen durch das Zusammenspiel vieler Gene. Hinzu kommt der Einfluss der Umwelt: Ernährung, Aufzucht, Training und andere äußere Faktoren prägen die Entwicklung eines Hundes entscheidend mit. Die quantitative Genetik liefert die wissenschaftlichen Werkzeuge, um diese komplexen Zusammenhänge zu verstehen und für die praktische Zuchtarbeit nutzbar zu machen.
Die quantitative Genetik befasst sich mit Merkmalen, die sich in Zahlen ausdrücken lassen – zum Beispiel die Größe eines Hundes, die Länge seines Fangs, aber auch komplexere Eigenschaften wie die Ausprägung der Hüftgelenksdysplasie oder Verhaltensmerkmale, die sich in Punkteskalen bewerten lassen. Dies gilt sogar für Merkmale, die auf den ersten Blick qualitativ erscheinen: Fellfarben zum Beispiel lassen sich als Zahlenwerte kodieren, insbesondere, wenn man nicht nur etwa rote und schwarze Fellfarbe unterscheidet, sondern auch alle Abstufungen dazwischen berücksichtigt.
In diesem Kapitel lernen Sie, wie sich Eigenschaften von einer Generation zur nächsten vererben – typischerweise durch das Zusammenwirken vieler Gene. Sie werden verstehen, warum der sichtbare Phänotyp – also das Erscheinungsbild und die messbaren Eigenschaften eines Hundes – nicht immer ein verlässlicher Hinweis auf seine Vererbungsleistung ist. Wir werden uns mit dem Konzept des Zuchtwertes beschäftigen, der angibt, was ein Hund tatsächlich an seine Nachkommen weitergeben kann.
Besonders wichtig für die praktische Zuchtarbeit ist das Zusammenspiel verschiedener Merkmale. Wie gehen wir damit um, wenn die Verbesserung einer Eigenschaft eine andere verschlechtert? Dies ist keine theoretische Frage, sondern tägliche Herausforderung in der Zuchtpraxis. Sie ist zum Beispiel dann relevant, wenn Sie bei einer brachyzephalen Rasse (d.h. einer Rasse mit kurzem Fang) den charakteristischen Kopf erhalten, gleichzeitig aber gesundheitliche Probleme loswerden möchten.
Die Konzepte der quantitativen Genetik erscheinen zunächst vielleicht abstrakt, aber sie sind der Schlüssel zum Verständnis moderner Zuchtmethoden. Mit diesem Wissen können Sie Ihre Zuchtentscheidungen auf eine wissenschaftliche Grundlage stellen und den Erfolg Ihrer Zuchtarbeit besser planen.
1. Grundlagen der Vererbung
1.1 Ein einfaches Beispiel: Die Fellfarbe
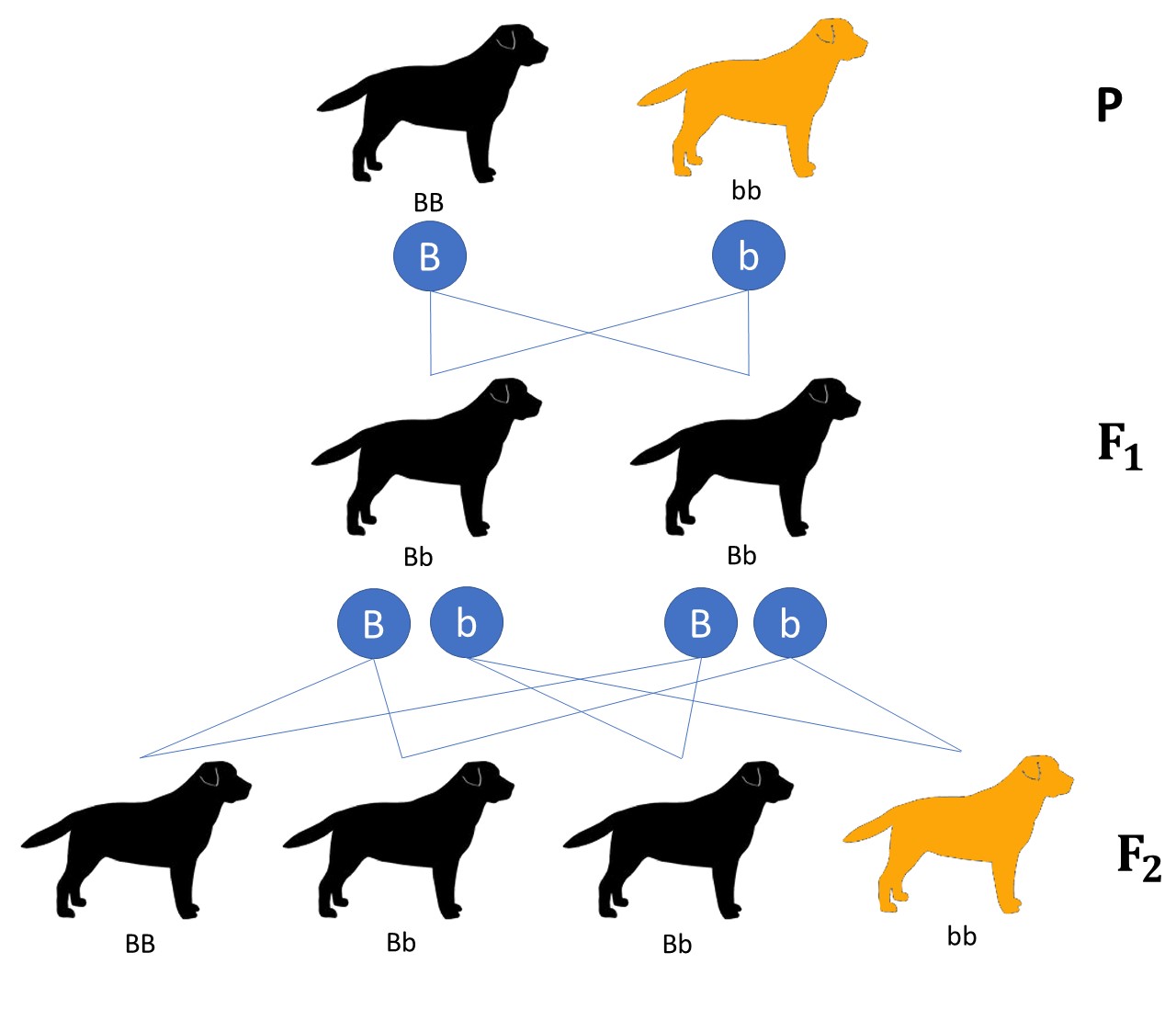
Dominanter Erbgang am Beispiel des Labrador Retriever
Um zu verstehen, wie quantitative Merkmale vererbt werden, betrachten wir zunächst ein einfaches Beispiel: die Vererbung der schwarzen Fellfarbe beim Labrador Retriever. Ein Hund erbt von jedem Elternteil je eine Kopie des Gens für die Fellfarbe. Die Variante für schwarze Farbe (B) ist dominant über die Variante für braune Farbe (b). Das bedeutet: Ein Hund mit der Kombination BB oder Bb wird schwarz, nur ein Hund mit der Kombination bb wird braun.
Die Weitergabe der Gene folgt den Mendelschen Regeln: Jeder Elternteil gibt zufällig eine seiner beiden Genkopien an jeden Nachkommen weiter. Ein schwarzer Hund mit der Kombination Bb vererbt also in der Hälfte der Fälle B und in der anderen Hälfte b. Wenn beide Eltern die Kombination Bb haben, dann werden im Durchschnitt drei Viertel der Welpen schwarz (BB oder Bb) und ein Viertel braun (bb).
1.2 Von einfachen zu komplexen Merkmalen
Die meisten Merkmale werden von mehr als einem Gen beeinflusst. Betrachten wir die Größe eines Hundes: Hier wirken viele Gene zusammen. Jedes dieser Gene kommt – wie das Farbgen – in verschiedenen Varianten vor, und jeder Hund erbt von jedem Elternteil je eine Variante. In der Regel addieren sich die Effekte der einzelnen Gene dabei auf.
Nehmen wir zum Beispiel an, es gäbe nur drei Gene für die Körpergröße, deren Genvarianten wir A/a, C/c und D/d nennen. Die Großbuchstaben stehen für Varianten, die das Wachstum fördern, die Kleinbuchstaben für Varianten, die das Wachstum weniger fördern. Ein Hund mit der Kombination AACCDD würde dann besonders groß, einer mit aaccdd besonders klein. Alle anderen Kombinationen führen zu Größen dazwischen. Je mehr wachstumsfördernde Varianten ein Hund hat, desto größer wird er. In Wirklichkeit sind jedoch noch viel mehr Gene an der Größenentwicklung beteiligt.
Zum Einfluss der Gene kommt der Einfluss der Umwelt hinzu: Ein Hund, der als Welpe nicht bedarfsgerecht ernährt wird, erreicht nicht die Größe, die seine Gene eigentlich ermöglichen würden. Die tatsächlich gemessene Größe eines Hundes – sein Phänotyp – ist also das Ergebnis des Zusammenspiels seiner Gene (seines Genotyps) mit den Umwelteinflüssen.
1.3 Ausblick
Auch wenn die einzelnen Gene auf unterschiedliche Weise wirken können – manche dominant, manche rezessiv – lassen sich ihre durchschnittlichen Effekte auf die nächste Generation immer durch ihre Substitutionseffekte beschreiben, die im nächsten Kapitel eingeführt werden. Diese Substitutionseffekte sind für die Zucht besonders wichtig, weil sie vorhersagen, wie sich ein Merkmal von einer Generation zur nächsten entwickeln wird.
Mit diesem Verständnis der grundlegenden Vererbungsmechanismen können wir uns nun den speziellen Konzepten der quantitativen Genetik zuwenden: Was ist der Zuchtwert eines Hundes? Wie stark ist der Einfluss der Gene im Vergleich zur Umwelt? Und wie können wir dieses Wissen für die Zuchtarbeit nutzen?
2. Genetische Grundbegriffe
Nachdem wir die grundlegenden Vererbungsmechanismen kennengelernt haben, werden wir nun die wichtigsten Begriffe der quantitativen Genetik einführen. Diese Begriffe helfen uns, die Vererbung von Merkmalen präzise zu beschreiben und vorherzusagen.
Beginnen wir mit einem konkreten Beispiel: In einer Population von Deutschen Schäferhunden beträgt die durchschnittliche Widerristhöhe der Rüden 63 cm. Einzelne Rüden sind größer oder kleiner als dieser Durchschnitt. Die Abweichung eines Hundes vom Populationsmittel kann verschiedene Ursachen haben: seine Gene, die Umwelteinflüsse während seiner Entwicklung oder eine Kombination von beidem. Das Ausmaß in dem die Hunde ihre Größenabweichungen an die nächste Generation vererben, hängt von den Substitutionseffekten ihrer Gene ab.
2.2 Genotypwert und Zuchtwert
Die Effekte aller Gene eines Hundes $i$ auf ein Merkmal addieren sich zu seinem Genotypwert $g_i$ auf. Der Genotypwert für das Merkmal „Größe“ gibt somit an, welche Größe ein Hund aufgrund seiner Gene erreichen würde. Der Zuchtwert $a_i$ des Hundes sagt hingegen voraus, wie er das Merkmal an seine Nachkommen vererbt.
Um den Zuchtwert zu verstehen, müssen wir uns ansehen, wie einzelne Gene vererbt werden: Wir nehmen an, dass es an jedem Genort $n$ eine Genvariante A0 und eine alternative Genvariante A1 gibt. Ein Hund kann von der alternativen Variante null, eine oder zwei Kopien tragen.
Der Effekt $\alpha_n$ der alternativen Genvariante A1 auf den Zuchtwert eines Hundes wird als der Substitutionseffekt des Gens bezeichnet. Er gibt an, wie stark sich der Genotypwert eines Nachkommen im Mittel ändern würde, wenn er statt der Variante A0 die Variante A1 vom oben betrachteten Elternteil geerbt hätte. Die Größe dieser Änderung hängt davon ab, welche Variante der Hund von seinem anderen Elternteil geerbt hat. Der Substitutionseffekt ist der Durchschnitt über alle möglichen Anpaarungspartner.
Die Substitutionseffekte aller Genorte addieren sich auf. Wären die Substitutionseffekte $\alpha_n$ aller Genorte bekannt, könnte man den Zuchtwert eines Hundes mit folgender Formel berechnen:
\[a_i = \sum_n (x_{in}-\bar{x}_n)\alpha_n,\]
wobei über alle Genorte $n$ summiert wird. Der Wert $x_{in}$ ist die Anzahl der Kopien, die der Hund $i$ von der alternativen Variante am Genort $n$ trägt (0, 1 oder 2) und $\bar{x}_n$ ist der Mittelwert dieser Anzahl in der Population. Der Abzug von $\bar{x}$ bewirkt, dass die Zuchtwerte im Mittel 0 sind.
Ein Rüde mit einem Zuchtwert von +2 cm für Größe wird Nachkommen haben, die im Durchschnitt 1 cm größer sind als der Populationsdurchschnitt – nur die Hälfte des Zuchtwertes wird weitergegeben, da die andere Hälfte der Gene von der Hündin kommt. Der Zuchtwert ist damit die entscheidende Größe für die Zuchtarbeit: Er sagt voraus, wie sich unsere Zuchtentscheidungen auf die nächste Generation auswirken werden.
2.1 Der Substitutionseffekt eines Gens
2.1.1 Additive und dominante Genwirkung
Der Zuchtwert eines Hundes ergibt sich aus der Summe der Substitutionseffekte aller seiner Gene. Aber wie berechnet sich der Substitutionseffekt eines einzelnen Gens? Wie wir im letzten Kapitel gesehen haben, ist der Substitutionseffekt $α$ definiert als der erwartete Unterschied im Genotypwert zweier Hunde, die sich nur in der vom (sagen wir) Vater geerbten Genvariante unterscheiden und deren mütterliche Genvariante von einem zufällig gewählten Anpaarungspartner stammt.
Wir betrachten ein Gen das unabhängig von anderen Genen wirkt. An diesem Genort gibt es zwei mögliche Varianten: A0 und A1, wobei wir A1 als die alternative Variante bezeichnen. Die Wirkung des Gens auf ein Merkmal wird durch zwei Parameter beschrieben:
- Den additiven Effekt $a$: Er gibt an, wie stark sich die Varianten bei reinerbigen Hunden auswirken
- Den Dominanzeffekt $d$: Er beschreibt, wie sich die Varianten bei mischerbigen Hunden auswirken
Die Wirkung des Gens läßt sich am besten anhand eines konkreten Merkmals erläutern. Wir nehmen daher an, dass das Gen einen Effekt auf die Körpergröße von Hunden hat. Ein Hund mit zwei Kopien der Variante A0 (Genotyp A0A0) wird im Durchschnitt um $a$ Zentimeter kleiner sein und ein Hund mit zwei Kopien der alternativen Variante (A1A1) wird um $a$ Zentimeter größer sein als der Mittelwert beider Hunde. Ein mischerbiger Hund mit beiden Varianten (A0A1 oder A1A0) wird durch den Dominanzeffekt beeinflusst und wird um $d$ Zentimeter größer sein.

Die allgemeine Formel für den Substitutionseffekt lautet in diesem Fall:
\[\alpha = a + (q – p)d.\]
Dabei ist $q$ die Häufigkeit der Variante A0 bei den infrage kommenden Anpaarungspartnern und $p=1-q$ ist die Häufigkeit der alternativen Variante A1.
2.1.2 Berechnung des Substitutionseffektes
Im diesem Abschnitt wollen wir die Formel für den Substitutionseffekt mathematisch herleiten. Wenn Sie sich nicht für die Herleitung interessieren, können Sie direkt zu Kapitel 2.1.3 springen. Um den Substitutionseffekt zu berechnen, vergleichen wir zwei Hunde:
- Hund 0 hat die Variante A0 vom Vater geerbt
- Hund 1 hat die Variante A1 vom Vater geerbt
- Beide haben eine zufällige Variante von der Mutter geerbt
Die Herleitung der Formel erfolgt in zwei Schritten. Zunächst berechnen wir den erwarteten Beitrag des Genorts zum Genotypwert von Hund 0:
- Mit Wahrscheinlichkeit $q$ hat er Genotyp A0A0 und damit Beitrag $-a$
- Mit Wahrscheinlichkeit $p$ hat er Genotyp A0A1 und damit Beitrag $d$
- Der erwartete Beitrag $α_0$ ist somit: $α_0 = q(-a) + pd$.
Dann berechnen wir den erwarteten Beitrag des Genorts zum Genotypwert von Hund 1:
- Mit Wahrscheinlichkeit $q$ hat er Genotyp A1A0 und damit Beitrag $d$
- Mit Wahrscheinlichkeit $p$ hat er Genotyp A1A1 und damit Beitrag $a$
- Der erwartete Beitrag $α_1$ ist somit: $α_1 = qd + pa$.

Der Substitutionseffekt $α$ ist die Differenz dieser erwarteten Beiträge:
\[\begin{align*}\alpha &= \alpha_1 – \alpha_0 \\ &= (q d + p a) – \big(q(-a) + p d\big) \\ &= q d + p a + q a – p d \\ &= (p + q)a + (q – p)d \\ &= a + (q – p)d. \end{align*}\]
2.1.3 Folgerungen für die Hundezucht
Betrachten wir einige Spezialfälle, die in der Hundezucht häufig vorkommen:
Fall 1: A1 ist vollständig rezessiv und erwünscht
Hier führt nur der Genotyp A1A1 zum erwünschten Effekt und wir haben $d=-a$. Setzen wir den Wert in die Formel ein, erhalten wir $α = 2pa$. Der Substitutionseffekt ist also stark von der Häufigkeit der Genvariante A1 abhängig. Ist die erwünschte Genvariante selten ($p$ nahe 0), ist der Substitutionseffekt nahe 0 und eine Selektion anhand von Zuchtwerten sehr ineffizient. In diesem Fall kann Linienzucht weiterhelfen: Man erstellt eine Teilpopulation, in der das Allel A1 häufiger vorkommt, und selektiert zunächst nur innerhalb dieser Teilpopulation auf A1. Dadurch erhöht sich $p$ und damit auch der Substitutionseffekt.
Fall 2: A1 ist vollständig dominant und erwünscht
Hier ist die Variante A0 rezessiv und unerwünscht und wir haben $d=a$. Der Substitutionseffekt des Gens ist daher $α = 2qa$. Je häufiger die unerwünschte rezessive Variante A0 ist (also je größer $q$ ist), desto größer ist der Substitutionseffekt. Die Selektion gegen A0 ist also besonders effizient, wenn A0 noch häufig ist. Mit abnehmender Häufigkeit von A0 wird die Selektion immer ineffizienter. Dies erklärt, warum sich unerwünschte rezessive Genvarianten oft lange in einer Population halten können.
Fall 3: Keine Dominanz
Hier ist $d=0$. In diesem Fall ist $α = a$, unabhängig von den Genfrequenzen. Der Substitutionseffekt ist konstant und die Effizienz der Selektion für oder gegen eine Genvariante hängt nicht von ihrer Häufigkeit ab.
Diese Erkenntnisse haben praktische Konsequenzen für die Zuchtarbeit:
- Erwünschte rezessive Genvarianten lassen sich durch Linienzucht effizienter etablieren als durch Zufallspaarung
- Unerwünschte rezessive Genvarianten können anfangs effizient reduziert werden, ihre vollständige Elimination ist jedoch schwierig
- Bei Genen ohne Dominanz ist die Selektion in jeder Phase gleich effizient.
2.3 Umweltabweichung und Residualabweichung
Die Differenz zwischen dem tatsächlich gemessenen Wert $y_i$ (Phänotypwert) eines Tieres $i$ und seinem Genotypwert nennt man die Umweltabweichung $e_i$. Man hat also
\[y_i = g_i + e_i.\]
Bei statistischen Auswirkungen modelliert man die nicht-genetischen Effekte oft nicht direkt, sondern nimmt an, dass sie Teil des Residuums sind, das auch als $e_i$ bezeichnet wird. In diesem Fall hat man die alternative Darstellung
\[y_i = \mu + a_i + e_i,\]
wobei $\mu$ der Populationsmittelwert ist.
Diese Konzepte – Substitutionseffekt, Genotypwert, Zuchtwert und Umweltabweichung – bilden das Fundament für das Verständnis der quantitativen Genetik. Im nächsten Kapitel werden wir sehen, wie sich diese Werte in einer Population verteilen und wie stark ihr Einfluss auf die Merkmalsausprägung ist.
3. Varianzkomponenten
Bisher haben wir einzelne Hunde betrachtet und deren Abweichungen vom Populationsmittel untersucht. Für die Zuchtarbeit ist aber auch wichtig zu wissen, wie stark diese Abweichungen in der gesamten Population streuen. Diese Streuung wird in der Statistik als Varianz bezeichnet. Die Varianz ist ein Maß dafür, wie weit die einzelnen Werte im Durchschnitt vom Mittelwert entfernt sind.
3.1 Die phänotypische Varianz
Bleiben wir bei unserem Beispiel der Widerristhöhe beim Deutschen Schäferhund. Wenn wir die Höhe vieler Rüden messen, werden wir unterschiedliche Werte finden. Die Varianz dieser gemessenen Werte nennt man die phänotypische Varianz $V_P$. Sie beschreibt, wie stark die tatsächlich gemessenen Werte um den Populationsdurchschnitt streuen.
3.2 Die genetischen Varianzen
Die phänotypische Varianz lässt sich in verschiedene Komponenten zerlegen. Die wichtigste ist die genetische Varianz $V_G$: Sie beschreibt, wie stark die Genotypwerte in der Population streuen. Ein Teil dieser genetischen Varianz ist die additive genetische Varianz oder Zuchtwert-Varianz $V_A$: Sie gibt an, wie stark die Zuchtwerte in der Population streuen.
Die additive genetische Varianz ist für die Zucht besonders wichtig: Je größer sie ist, desto mehr Spielraum haben wir für die Selektion. Wenn zum Beispiel die Zuchtwerte für die Widerristhöhe stark streuen, können wir besonders große oder besonders kleine Hunde zur Zucht auswählen und erwarten eine entsprechende Reaktion in der nächsten Generation.
Der Teil der genetischen Varianz, der nicht additiv ist, wird durch Dominanzeffekte und Wechselwirkungen zwischen verschiedenen Genorten (Epistasie) verursacht. Diese Varianzkomponenten sind für die Zucht weniger wichtig, da sie sich nicht gezielt von einer Generation zur nächsten weitergeben lassen, es sei denn durch gezielte Anpaarungsplanung.
3.3 Umweltvarianz und Residualvarianz
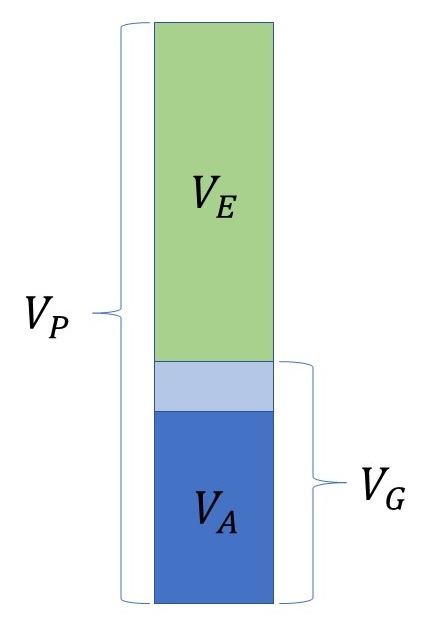
Die Umweltvarianz $V_E$ umfasst in die Effekte aller nicht-genetischen Einflüsse auf das Merkmal. Bei der Widerristhöhe wären das zum Beispiel Unterschiede in der Ernährung während des Wachstums oder Erkrankungen, die das Wachstum beeinflussen. Man hat also
\[V_P = V_G + V_E.\]
Die additive genetische Varianz ist Teil der genetischen Varianz. Man hat also: $V_A \leq V_G$. Die nicht-additiven genetischen Effekte werden bei statistischen Modellierungen jedoch oft vernachlässigt. In solch einem Fall nennt man die Differenz zwischen der phänotypischen Varianz und der additiv genetischen Varianz die Residualvarianz, die ebenfalls mit $V_E$ bezeichnet wird, und man hat:
\[V_P = V_A + V_E.\]
3.4 Die Bedeutung der Varianzkomponenten für die Zucht
Das Verhältnis der verschiedenen Varianzkomponenten zueinander ist für Züchter aus mehreren Gründen wichtig:
- Die additive genetische Varianz bestimmt, wie schnell wir durch Selektion züchterische Fortschritte erzielen können. Je größer ihr Anteil an der Gesamtvarianz ist, desto effektiver ist die Selektion.
- Eine große Umweltvarianz erschwert die Zuchtwahl, weil der Phänotyp dann weniger über den Zuchtwert aussagt. Wenn zum Beispiel Unterschiede in der Aufzucht einen starken Einfluss auf die Größe haben, ist es schwieriger, die genetisch großen Hunde zu erkennen.
- Eine hohe additive Varianz ist nicht immer von Vorteil. Wenn das Populationsmittel bereits nahe am gewünschten Optimum liegt, bedeutet eine hohe additive Varianz auch, dass unerwünschte Abweichungen vom Optimum häufig vorkommen. In diesem Fall ist eine niedrigere Varianz vorteilhaft, da sie die Population stabiler um das Optimum hält.
- Eine zu geringe genetische Varianz kann ein Warnsignal sein: Sie könnte bedeuten, dass die genetische Vielfalt in der Population abnimmt, was langfristig zu Problemen führen kann.
Im nächsten Kapitel werden wir sehen, wie sich das Verhältnis von additiver genetischer Varianz zur phänotypischen Varianz in der Erblichkeit eines Merkmals ausdrückt und wie wir dieses Konzept in der praktischen Zuchtarbeit nutzen können.
4. Erblichkeit und Zuchtfortschritt
Die Erblichkeit $h^2$ (engl: heritability) ist eine der wichtigsten Kenngrößen in der Tierzucht. Sie ist definiert als der Anteil der additiven genetischen Varianz an der phänotypischen Varianz, also $h^2=V_A/V_P$. Anders ausgedrückt: Die Erblichkeit gibt an, welcher Anteil der beobachteten Unterschiede zwischen den Tieren auf Unterschiede in ihren Zuchtwerten zurückzuführen ist.
4.1 Interpretation der Erblichkeit
Die Erblichkeit wird als Zahl zwischen 0 und 1 angegeben, oft auch in Prozent ausgedrückt. Eine Erblichkeit von 0,4 oder 40% bedeutet, dass 40% der beobachteten Unterschiede zwischen den Hunden genetisch bedingt sind und an die Nachkommen weitergegeben werden können. Die restlichen 60% der Unterschiede gehen auf Umwelteinflüsse und nicht-additive genetische Effekte zurück.
Wichtig ist: Die Erblichkeit ist keine fixe Eigenschaft eines Merkmals, sondern hängt von der Population und den Umweltbedingungen ab. In einer Population, in der alle Hunde unter sehr ähnlichen Bedingungen aufwachsen, wird die Erblichkeit höher sein als in einer Population mit sehr unterschiedlichen Haltungsbedingungen. Der Grund: Gleichmäßigere Umweltbedingungen verringern die Umweltvarianz und erhöhen damit den relativen Anteil der genetischen Varianz.
4.2 Typische Erblichkeitswerte in der Hundezucht
Merkmale unterscheiden sich stark in ihrer Erblichkeit:
- Körpermaße wie die Widerristhöhe haben oft hohe Erblichkeiten (0,4-0,6)
- Gesundheitsmerkmale wie die Hüftgelenksdysplasie zeigen mittlere Erblichkeiten (0,2-0,4)
- Verhaltensmerkmale und Fruchtbarkeitsmerkmale haben oft niedrige Erblichkeiten (0,1-0,2)
Diese Unterschiede erklären, warum die züchterische Verbesserung bei manchen Merkmalen schneller vorangeht als bei anderen.
4.3 Die Erblichkeit in der Züchtergleichung
Die Erblichkeit ist Teil der sogenannten Züchtergleichung (engl: breeder’s equation). Diese beschreibt den erwarteten Zuchtfortschritt $\Delta G$ pro Generation:
\[ \Delta G = h^2 S\]
Dabei ist das Selektionsdifferential $S$ die durchschnittliche Überlegenheit der ausgewählten Zuchttiere gegenüber dem Populationsmittel. Wenn wir zum Beispiel für die Zucht nur Hunde auswählen, die 2 cm größer sind als der Durchschnitt, und die Erblichkeit der Größe 0,5 beträgt, erwarten wir in der nächsten Generation eine durchschnittliche Größenzunahme von 1 cm.
4.4 Praktische Bedeutung für die Zuchtarbeit
Die Erblichkeit hilft bei wichtigen Zuchtentscheidungen:
- Bei Merkmalen mit hoher Erblichkeit kann man die Zuchttiere gut anhand ihres eigenen Phänotyps auswählen. Wenn ein Merkmal zu 60% erblich ist, wird sich die Überlegenheit eines Zuchttieres zu einem großen Teil in seinen Nachkommen wiederfinden.
- Bei Merkmalen mit niedriger Erblichkeit ist es wichtig, auch die Verwandtenleistung zu berücksichtigen. Wenn ein Merkmal nur zu 10% erblich ist, sagt der Phänotyp eines einzelnen Hundes wenig über seinen Zuchtwert aus.
- Die Erblichkeit bestimmt auch, wie schnell wir züchterische Fortschritte erwarten können. Bei hoher Erblichkeit können wir schneller züchterische Erfolge erzielen als bei niedriger Erblichkeit.
Im nächsten Kapitel werden wir sehen, wie sich diese Konzepte auf mehrere Merkmale erweitern lassen. Dabei werden wir lernen, wie Merkmale genetisch miteinander zusammenhängen können und was das für die praktische Zuchtarbeit bedeutet.
5. Gleichzeitige Verbesserung mehrerer Merkmale
Bisher haben wir einzelne Merkmale betrachtet. In der Zuchtpraxis müssen wir aber immer mehrere Merkmale gleichzeitig berücksichtigen. Beim Deutschen Schäferhund wollen wir zum Beispiel nicht nur die Größe optimieren, sondern auch Gesundheit, Wesen und andere Eigenschaften verbessern. Dafür müssen wir verstehen, wie diese Merkmale zusammenhängen.
5.1 Korrelationen und Kovarianzen
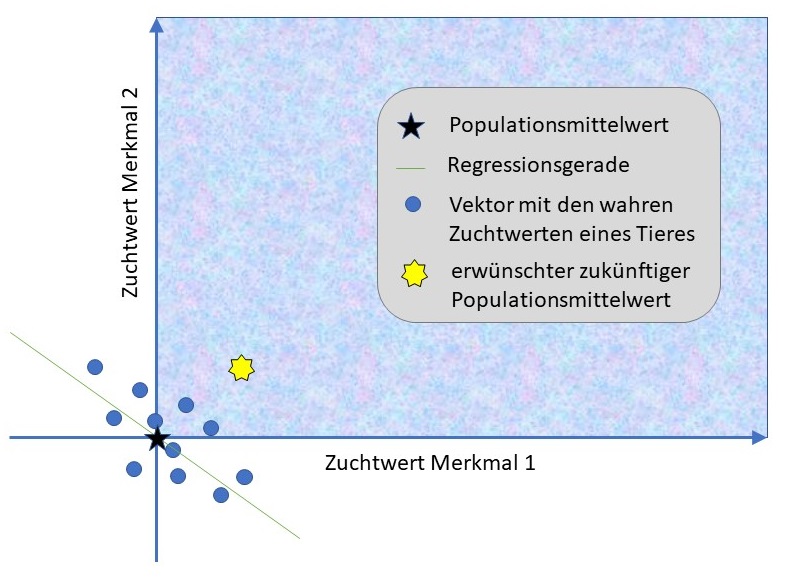
Die Abbildung zeigt zwei unvorteilhaft korrelierte Merkmale, die beide verbessert werden sollen.
Merkmale können genetisch miteinander korreliert sein. Das bedeutet, dass die Zuchtwerte verschiedener Merkmale nicht unabhängig voneinander sind. Eine genetische Korrelation entsteht auf zwei Wegen:
- Pleiotropie: Ein Gen beeinflusst mehrere Merkmale gleichzeitig
- Genkopplung: Gene für verschiedene Merkmale liegen auf dem gleichen Chromosom nahe beieinander und werden daher meist gemeinsam vererbt
Die genetische Korrelation $r^2$ zweier Merkmale wird wie ein Korrelationskoeffizient auf einer Skala von -1 bis +1 angegeben. Eine positive Korrelation bedeutet, dass die Merkmale sich gleichgerichtet entwickeln: Hunde mit überdurchschnittlichen Zuchtwerten für das eine Merkmal haben tendenziell auch überdurchschnittliche Zuchtwerte für das andere Merkmal. Bei einer negativen Korrelation entwickeln sich die Merkmale gegenläufig.
Eine genetische Korrelation von 0,5 bedeutet bei normalverteilten Zuchtwerten: Wenn ein Hund beim ersten Merkmal einen Zuchtwert hat, der eine Standardabweichung über dem Mittelwert liegt, dann liegt sein Zuchtwert für das zweite Merkmal im Durchschnitt eine halbe Standardabweichung über dem Mittelwert.
Bei vielen Hunderassen finden wir eine positive genetische Korrelation zwischen Körpergröße und Hüftgelenksdysplasie: Genetisch größere Hunde neigen häufiger zu Hüftproblemen. Dies erschwert es, gleichzeitig die gewünschte Größe zu erhalten und die Hüftgesundheit zu verbessern.
Ein anderes Beispiel ist die (oft behauptete) negative genetische Korrelation zwischen der Kürze des Fangs und der Atemwegsgesundheit bei brachyzephalen Rassen: Gene, die zu einem kürzeren Fang führen, beeinträchtigen oft auch die Atemwegsfunktion.
Die Korrelationen berechnen sich aus den Kovarianzen. Diese Informationen werden in Kovarianzmatrizen zusammengefasst. Die phänotypische Kovarianzmatrix $P$ enthält in der Diagonale die phänotypischen Varianzen der einzelnen Merkmale. Die anderen Einträge sind die phänotypischen Kovarianzen zwischen je zwei Merkmalen. Bei zwei Merkmalen sieht die Matrix so aus:
\[P=\begin{bmatrix} V_{P1} & \text{Cov}_{P12} \\ \text{Cov}_{P21} & V_{P2} \end{bmatrix}\]
Dabei ist $V_{P1}$ die phänotypische Varianz des ersten Merkmals, $V_{P2}$ die des zweiten Merkmals, und $\text{Cov}_{P12} = \text{Cov}_{P21}$ ist die phänotypische Kovarianz zwischen beiden Merkmalen. Genauso ist die genetische Kovarianzmatrix $G$ aufgebaut, nur dass sie die additiv genetischen Varianzen und Kovarianzen enthält:
\[G=\begin{bmatrix} V_{A1} & \text{Cov}_{A12} \\ \text{Cov}_{A21} & V_{A2} \end{bmatrix}\]
Die genetische Korrelation $r_{12}$ zwischen zwei Merkmalen hängt mit den Einträgen der genetischen Kovarianzmatrix wie folgt zusammen:
\[r_{12} = \frac{\text{Cov}_{A12}}{\sqrt{V_{A1}V_{A2}}}.\]
Kovarianzmatrizen werden vor allem dann genutzt, wenn Zuchtwerte für mehr als 2 Merkmale geschätzt werden sollen, weil sich mit ihnen dann die Notation vereinfachen lässt.
5.3 Der Selektionsindex
Wenn wir auf mehrere Merkmale gleichzeitig selektieren wollen, dann könnten wir einfach für jedes Merkmal eine Mindestanforderung festlegen und nur Hunde, die alle Anforderungen erfüllen, zur Zucht einsetzen. Dieses Vorgehen ist zwar weit verbreitet, aber ineffizient.
Effizienter ist die Selektion nach einem Selektionsindex. Der Selektionsindex gewichtet die Merkmale nach ihrer Wichtigkeit und fasst sie zu einem Gesamtwert zusammen. Hunde mit zu schlechtem Selektionsindex werden von der Zucht ausgeschlossen. Der Selektionsindex $I$ eines Hundes berechnet sich als
\[I=b_1y_1 + …. + b_M y_M,\]
wobei $M$ die Anzahl der Merkmale ist, der Vektor $b$ im Komponenten $b_1,…, b_M$ die Gewichte der Merkmale enthält und der Vektor $y$ mit Komponenten $y_1,…., y_M$ nach Möglichkeit die Zuchtwerte des Hundes in allen Merkmalen enthält.
Da in der Hundezucht aber häufig keine Zuchtwerte berechnet werden, kann man alternativ die Merkmalsausprägungen der Hunde selbst gewichten und aufsummieren. In diesem Fall ist $y_m$ die gemessene Merkmalsausprägung des Hundes für Merkmal $m$. In der Tat werden Zuchtwerte in der Hundezucht nur sehr selten berechnet, weshalb wir hier immer davon ausgehen, dass es sich bei $y$ um den Vektor mit den gemessenen Merkmalsausprägungen des Hundes handelt.
5.4 Der Selektionsindex mit Restriktion
Ein besonders wichtiges Werkzeug ist der Selektionsindex mit Restriktion (engl: restricted selection index). Er erlaubt es uns, bestimmte Merkmale zu verbessern, während andere unverändert bleiben sollen. Bei brachyzephalen Rassen könnte man damit zum Beispiel die Atemwegsgesundheit verbessern, ohne die charakteristische Kopfform zu verändern.
Die Konstruktion eines solchen Index erfordert, dass die Erblichkeiten aller beteiligten Merkmale und ihre genetischen Korrelationen geschätzt worden sind. Der Selektionsindex $I$ eines Hundes für zwei Merkmale mit Phänotypwerten $x_1$ und $x_2$ hat die Form:
\[I = b_1 x_1 + b_2 x_2\]
wobei die Gewichte $b_1$ und $b_2$ so gewählt werden, dass:
- der erwartete Zuchtfortschritt im ersten Merkmal null ist
- der erwartete Zuchtfortschritt im zweiten Merkmal maximal ist
Dies ist der Fall, wenn die Gewichte $b_1$ und $b_2$ die folgende Bedingung erfüllen:
\[\frac{b_1}{b_2} = – r \frac{h_2}{h_1} \frac{\sigma_{P2}}{\sigma_{P1}}.\]
Bitte beachten Sie, dass die Gleichung für den Fall hergeleitet worden ist, dass die Phänotypen der Hunde mit dem Index gewichtet werden und nicht ihre Zuchtwerte. Dabei sind:
- $h_1, h_2$: die Wurzeln aus den Erblichkeiten der Merkmale 1 und 2
- $r$: die genetische Korrelation zwischen den Merkmalen
- $\sigma_{P1}, \sigma_{P2}$: die phänotypischen Standardabweichungen der Merkmale.
Benutzt man diesen Index zur Selektion der Zuchttiere, wird sich das erste Merkmal im Durchschnitt nicht verändern, während das zweite Merkmal sich in die gewünschte Richtung entwickelt. Dieser Index ist ein Spezialfall des „Desired Gain“ Ansatzes, der an anderer Stelle vorgestellt wird.
5.5 Ausblick
Die gleichzeitige Selektion auf mehrere Merkmale ist immer schwieriger als die Selektion auf ein einzelnes Merkmal. Negative genetische Korrelationen zwischen erwünschten Eigenschaften zwingen uns zu Kompromissen. Je mehr Merkmale wir gleichzeitig verbessern wollen, desto langsamer wird der Zuchtfortschritt in jedem einzelnen Merkmal.
Mit diesem Wissen über die Vererbung quantitativer Merkmale können Sie Ihre Zuchtentscheidungen auf eine wissenschaftliche Grundlage stellen. Die vorgestellten Konzepte helfen Ihnen, realistische Zuchtziele zu setzen und die optimale Strategie zu ihrer Erreichung zu wählen.
6. Zusammenfassung
6.1 Die wichtigsten Konzepte
In diesem Kapitel zur quantitativen Genetik haben wir gelernt, dass die meisten für die Hundezucht wichtigen Merkmale von vielen Genen und von Umwelteinflüssen bestimmt werden. Die wichtigsten Konzepte sind:
- Der Substitutionseffekt eines Gens beschreibt, wie stark sich die Effekte der Genvarianten im Durchschnitt unterscheiden.
- Der Zuchtwert eines Hundes ergibt sich aus der Summe der Substitutionseffekte aller seiner Gene
- Die phänotypische Varianz lässt sich in genetische Varianz und Umweltvarianz zerlegen
- Die Erblichkeit ist der Anteil der additiven genetischen Varianz an der phänotypischen Varianz
- Genetische Korrelationen beschreiben den Zusammenhang zwischen verschiedenen Merkmalen
6.2 Praktische Bedeutung für die Hundezucht
Diese Konzepte sind für die praktische Zuchtarbeit aus mehreren Gründen wichtig:
- Sie helfen uns zu verstehen, warum der Phänotyp eines Hundes nicht immer ein verlässlicher Hinweis auf seine Vererbungsleistung ist.
- Die Erblichkeit eines Merkmals zeigt uns:
- wie gut wir den Zuchtwert eines Hundes anhand seines Phänotyps einschätzen können
- wie schnell wir züchterische Fortschritte erwarten können
- wie wichtig es ist, auch die Verwandtenleistung zu berücksichtigen
- Genetische Korrelationen erklären, warum:
- manche erwünschten Merkmale schwer gleichzeitig zu verbessern sind
- unerwünschte Merkmale manchmal als Nebenwirkung der Selektion auftreten
- spezielle Zuchtstrategien wie der Selectionsindex mit Restriktion nötig sein können.
6.3 Anwendung in der Zuchtpraxis
Für die praktische Anwendung sollten Sie beachten:
- Setzen Sie realistische Zuchtziele:
- Berücksichtigen Sie die Erblichkeiten der Merkmale
- Beachten Sie genetische Korrelationen zwischen den Merkmalen
- Planen Sie längerfristig, besonders bei Merkmalen mit niedriger Erblichkeit
- Wählen Sie die geeignete Zuchtstrategie:
- Bei hoher Erblichkeit: Eigenleistung ist ein guter Indikator
- Bei niedriger Erblichkeit: Verwandtenleistung stärker berücksichtigen
- Bei mehreren Merkmalen: Gewichtung nach Wichtigkeit und genetischen Zusammenhängen
- Überwachen Sie den Zuchtfortschritt:
- Dokumentieren Sie die Merkmalsausprägungen systematisch
- Überprüfen Sie regelmäßig, ob Sie sich Ihren Zuchtzielen nähern
- Passen Sie Ihre Zuchtstrategie bei Bedarf an
Die quantitative Genetik liefert uns das Handwerkszeug, um Zuchtentscheidungen auf eine wissenschaftliche Grundlage zu stellen. Sie hilft uns, die komplexen Zusammenhänge in der Vererbung zu verstehen und unsere Zuchtziele effektiv zu verfolgen.
